Du nouveau sur le nombre d’or

Solution mathématique simple applicable au groupe de pierres de la cathédrale de Laon encore énigmatique aujourd’hui. Suivi d’un développement logique aboutissant à la création d’un outil (une règle) simple et utile aux maîtres d’œuvre, pour la mise en proportion de leurs bâtiments. Suivra une application sur le relevé d’une façade du Petit Trianon qui semble convaincante.

1. Analyse des pierres de la cathédrale de Laon
2. La règle
3. Un hasard ?
4. Mise à l’épreuve
5. Compléments
   • Relevé des pierres de la cathédrale de Laon
   • Réflexion sur le sens donné par leur disposition
   • Une reconstitution des dimensions théories de la cathédrale est-elle possible ?

Les pierres de la cathédrale de Laon

Un essai de déchiffrement

Prenons la construction géométrique la plus élémentaire pour entrer dans le monde du nombre d’or (φ) : √5

Cette construction permet de définir deux modules. Le plus grand d’’entre eux est l’expression élémentaire du carré, le plus petit, l’expression d’un nombre irrationnel.
Le rapport proportionnel du double carré M0 avec son complément m0, constituants du rectangle √5, est √5 -2 = 0.236.. = 1/φ³

Avec ces 2 modules élémentaires, voyons quelles partitions du carré nous sont offertes.
Choisissons arbitrairement le nombre 4, (le carré ayant ce nombre de côtés …)
Donc, 4 grands modules et 4 petits modules additionnés pourraient définir les dimensions d’un hypothétique carré de base constitué par les pierres de Laon.

Voyons ce que cela donne…

Nous avons précisément les dimensions des pierres de la cathédrale de Laon à l’axe des joints.

Maintenant que le contact est pris avec les admirables constructeurs de la cathédrale, et que nous sommes probablement en possession de la clé de l’outil des Maîtres d’œuvre, continuons notre chemin ….

Voyons combien de modules m0 peu-t-on aligner dans M0 et qu’est donc que ce petit espace restant ? Nommons le m ; il est égal à 2 – 8 x (√5 – 2) = 0.11145618.

et alignement de modules semblables, précédé d’un petit espace encore indéfini, évoque une règle graduée. Est ce qu’une ‘’simple’’ règle graduée susciterait tant de mystères ?

Une approche détournée pourrait enrichir notre propos de données supplémentaires et confirmer l’intérêt de cette première approche.

La règle

Cherchons un module intermédiaire entre M0 et m0 tout en restant dans l’homogénéité numérique avec le rapport suivant: φ + φ / φ x φ
où m0 est multiplié par φ x φ = 0.618..
où M0 est divisé par φ + φ = 0.618..

0,618… = 1/φ = A

Prenons A comme élément primaire d’une grille harmonique.
La particularité de cette grille vient de la répartition, sur les deux axes x et y, de deux éléments A et a (a = A/φ) selon le rythme suivant: … A a A A a …

Une autre caractéristique de cette grille est qu’elle contient tous les rectangles liés à √5.

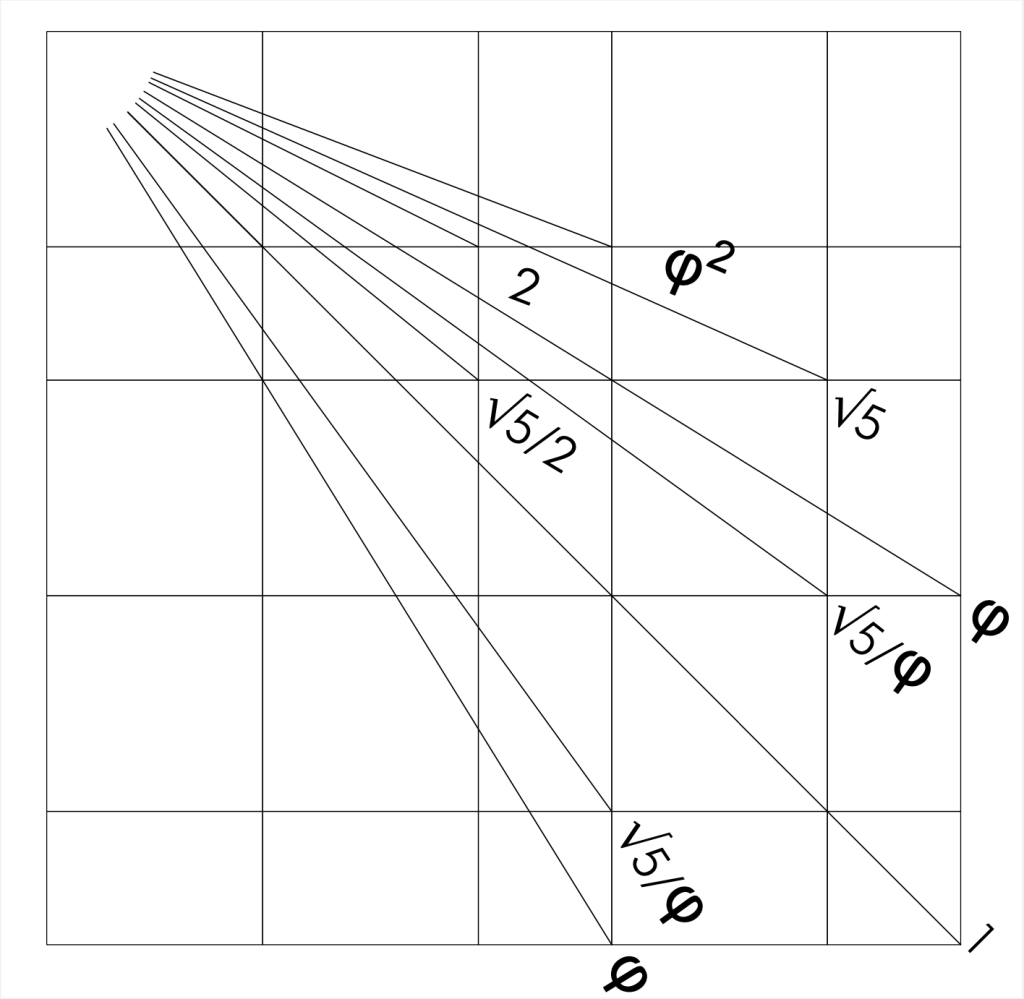
Voyons maintenant quels rapports cette grille entretient avec les modules M0 et m0 et éventuellement avec la petite partie résiduelle m. Notons que cette configuration correspond au demi côté du carré de base.

Dans la première partie de l’exposé, l’unité de base correspondait au rayon de M0. Dans cette seconde partie, c’est le module A qui prend, provisoirement, ce rôle.

Dès lors
M0 = A x (φ + φ) = A x 3.236…
m0 = A / φ² = A x 0.382..
m = M0 – (8 x m0) Si A = 1 alors m = 3.236.. – (8x 0.382..) = 2φ – (1/φ²) = 0.1803..
m0 / m = 0.382 / 0.1803 = 2.118 donc le rapport entre m et m0 est de (√5 / 2) + 1

Nous découvrons que m est en fait l’unité de base de notre système.

Ainsi nous pouvons tenter d’esquisser une règle dont toutes les mesures devront être prises à partir de son extrémité.
Rappelons que sa longueur correspond au demi côté du carré de base.

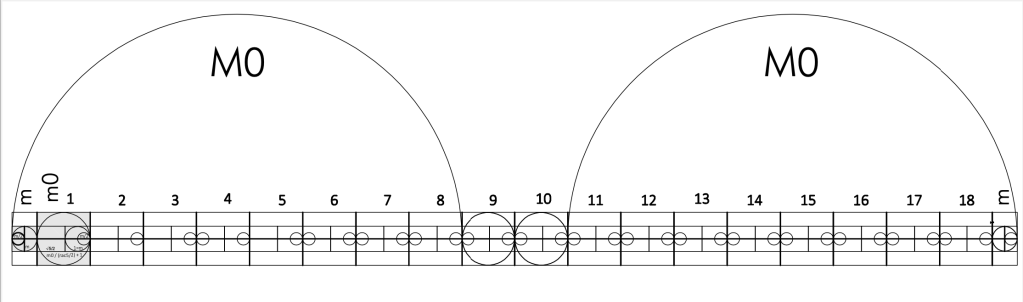
Après cet itinéraire dans les méandres du nombre d’or, reposons nous en constatant la grande simplicité de la construction de la règle :

Les deux cotes utiles à la construction de la règle m et (√5 x m / 2) – m sont données par la diagonale du double carré et son côté.

En définissant, en premier lieu, le carré de base d’une composition, il faudra, pour définir m, en passer par une légère approximation en déduisant du 1/4 du côté du carré de base le 1 % de sa longueur, puis diviser le reste en 19 segments égaux.

Reste le teste : une démonstration à l’aide d’un relevé précis d’une façade du Petit Trianon

Un hasard ?

Mais avant de faire ce test, de ce qui pourrait devenir un outil très intéressant à maints points de vue, retrouvons notre carré de base défini par les pierres de la cathédrale de Laon et examinons ses rapports avec la grille harmonique.

Traçons un cercle, dont le diamètre correspond au demi côté du carré de base, au centre de la composition. Puis un carré défini par la grille harmonique, selon la figure ci-dessous, et déplaçons enfin le cercle sur la base du carré.

Et …. une surprise !

En faisant correspondre le diamètre du cercle dessiné par Léonard de Vinci, représentant un homme inscrit à la fois dans un cercle et dans un carré, le carré du dessin correspond, avec une étonnante précision, à la figure qu nous venons de concevoir.
Remarquable est aussi la correspondance de la grille harmonique avec les différentes parties du corps.

Mise à l’épreuve de la règle harmonique

sur le relevé de la façade ouest du Petit Trianon

Prenons nos outils : la liste des dimensions générée par la règle harmonique, le carré de base et relevé de la façade est du Petit Trianon.

Étape 1 :dimensionner le carré de base

En prenant comme référence la hauteur de la façade entre le soubassement et l’entablement et en conservant la géométrie des pierres de Laon on trouve à la fois les axes des colonnes et des fenêtres mais aussi le niveau supérieur des fenêtres de l’étage noble. Le choix du carré de base étant adopté nous allons dimensionner la règle.

Étape 2 : Situer les fenêtres latérales, définir les limites du corps de bâtiment.

Dimensionner l’entablement, la balustrade de couronnement, le soubassement et sa balustrade.

Étape 3 : Dimensionner les ouvertures, le décrochement de l’avant corps central.

Dimensionner les détails de la modénature.

Vue d’ensemble des modules

Divers

Rapports entres échelles.

Notes :
Les cotes n’ont pas été vérifiées sur place ; la précision de celles-ci est dépendante du relevé et de la résolution de son image.
Par contre la précision des modules et de leurs raccords, calculés par l’ordinateur est absolue.

Les modules

Liste des modules, supposés avoir été mis en œuvre afin d’harmoniser les dimensions des éléments constitutifs des façades du Petit Trianon.
(non exhaustif)

On a la série M0-m0 correspondant à l’échelle définie par le carré de base
Et une autre série correspondant à l’échelle définie par le carré de base / φ²

Tableaux des modules et leurs dimensions

Relevé des pierres de la cathédrale de Laon

Les trait d’axes sur les joint correspondent à la géométrie décrite plus haut.

Observons que pierres ont, entre elles, des joints remarquablement large alors qu’elles sont parfaitement ajustées sur le périmètre du cadre. Y aurait-il un à cette différence de traitement des raccords entre les pierres ?
Aventurons-nous à faire une hypothèse: la disposition des des pierres, avec leurs larges joints, pourrait correspondre à un schéma, alors que le carré formé par le périmètre bien ajusté nous indiquerait une cote précise.

Développons cette hypothèse

Pourrait-on, grâce aux pierres, retrouver le système harmonique de la cathédrale ?

Tableaux des modules et leurs dimensions (cathédrale de Laon)

Et un mot pour terminer :

Tout au long de ma pratique architecturale j’ai eu le soucis de respecter un bon équilibre dimensionnel. C’est ce qui m’a amené à développer une analyse géométrique du nombre d’or, et ainsi à me doter d’une instrumentation ad hoc.
Ces bricolage s’avéraient utiles mais jamais pleinement satisfaisants sur le plan formel, et partant, étaient en perpétuelle évolution.
Pourtant je n’était pas loin du but. Je l’ai atteint grâce a l’examen de la configuration des pierres de la cathédrale de Laon.

François Anex
Genève, le 2 octobre 2024

courriel : dunouveausurlenombredor@bluewin.ch